Portfolio optimization for low risk investors

Person pointing at a positive chart with a globe in the background

With the rise in popularity of smart beta strategies, minimum-variance investing has moved into the spotlight of the financial industry.

The challenge

The path towards portfolio optimization is one strewn with challenges - and with what seems like a rolling conveyor of proposed solutions tumbling off the belt in academia, the challenge for us as practitioners becomes actually selecting one. But our quest towards selecting that single “best” strategy may be what’s clouding our vision. Even what appears to be a well-developed strategy ex-ante, may perform poorly in reality. After all, financial markets behave erratically and dynamically as we have all observed through moody downturns and seemingly hope-fueled gains during the pandemic. The solution? Consider ditching the single strategy approach.

‍

Our solution

Think of it as bringing the benefits of diversification from the portfolio to the estimation level, thereby overcoming the strategy selection problem. Our “smart”- optimization approach averages the plethora of minimum-variance strategies and leverages the time-series properties of returns. Through extensive testing, this proposed averaging rule achieves a lower out-of-sample portfolio standard deviation and higher risk-adjusted performance than any competing minimum-variance strategy. It not only offers sizable diversification benefits, but also lower turnover and less short interest. Given the nature of this approach, it is best suited to those seeking a low risk / low volatility strategy including conservative investors, pension funds and insurance solutions.

‍

Solution details

Even the most sophisticated portfolio optimization techniques rarely outperform an equally distributed portfolio strategy out-of-sample. This is due to the inherent estimation errors stemming from the estimation of the covariance matrix. Various estimators have been proposed to reduce the estimation error whereby the estimation errors of these estimators are lowly correlated with each other. Averaging exploits this low correlation by combining the unbiased sample estimator with a multitude of structured estimators. Essentially, if estimation errors can be reduced by combining the sample with one structured estimator, averaging over multiple estimators should offer further diversification potential. This approach combines the individual estimators such that the expected out-of-sample variance of the corresponding minimum-variance portfolio is minimized. In a simulation study, we show that this leads to favorable distributions for out-of-sample standard deviation and Sharpe ratio as shown in Figures 1 and 2 compared to existing strategies.

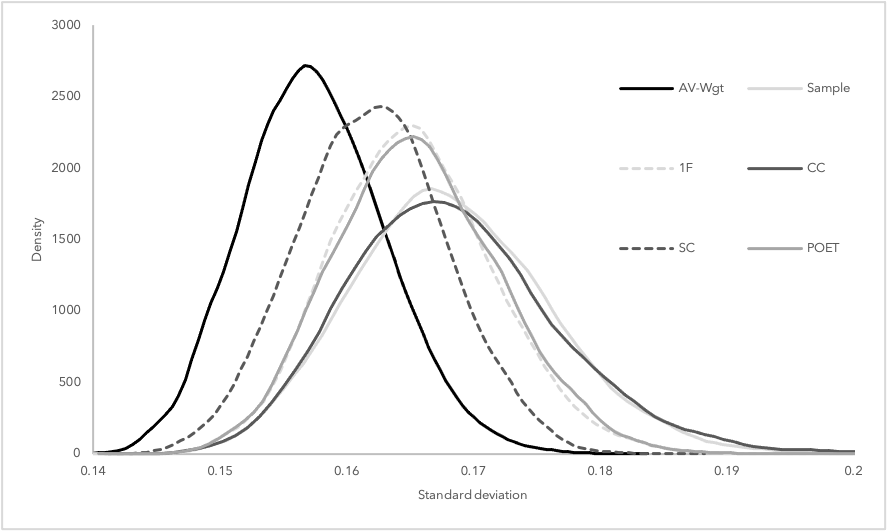
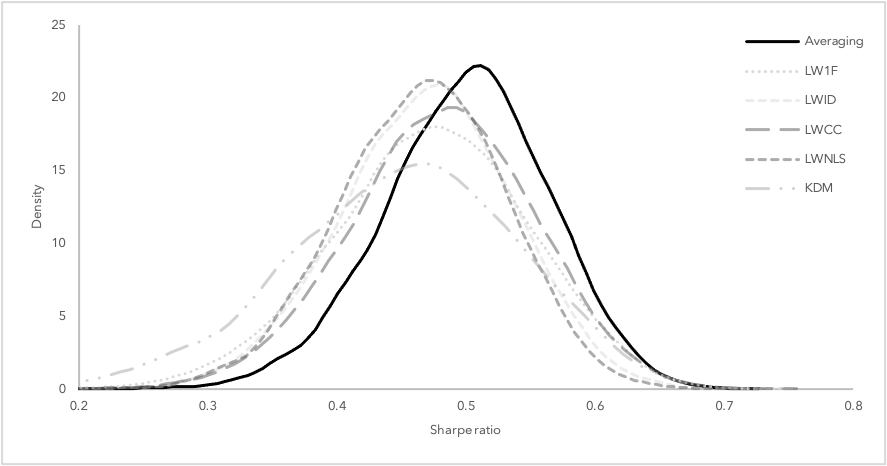
Figure 1 Distribution of Out-of-Sample Standard Deviations

Figure 2 Distribution of Out-of-Sample Sharpe Ratios

‍

The results are robust to transaction costs and the framework is flexible to be extended with additional restrictions like short-sale constraints or alternative averaging approaches.

‍

If you would like to learn more about the solution or discuss how this approach could benefit your clients and your organization, please contact us.

‍

Disclaimer

This report was written and produced by Fintama AG. Research discussed herein was conducted as part of Managing Partner, Christian Koeppel’s doctoral thesis in collaboration with Prof. Dr. Roland Füss from University of St. Gallen and Prof. Dr. Felix Miebs from Cologne University of Applied Science. Individual teams and researchers may hold different views and suggest different approaches for different clients. There are risks associated with any investment approach, and past performance is no guarantee for future returns.